Last wins - DPChallenge Forums

01/28/2014 03:24:50 PM · #23526

Spork sent you in his place...there or the re-education camp

Spork wins.

01/28/2014 03:52:35 PM · #23527

Spork has not won...

01/28/2014 04:00:41 PM · #23528

You, as usual, are wrong.

Spork wins.

01/28/2014 04:50:53 PM · #23529

Two wrongs make me right. I win.

Olympus 12-50mm f/3.5-6.3 MZuiko Digital ED EZ

01/28/2014 05:58:24 PM · #23530

I still win

LinMalAng

Panasonic Lumix DMC-GF1

01/28/2014 06:02:54 PM · #23531

I was thinking that instead of a DP challenge for digital photography that this has actually become a who does the best photo shopping contest. Did I win? Lol

01/28/2014 06:38:21 PM · #23532

Briefly. Very briefly.

Canon EF 200mm f/2.8 L II USM Lens

01/28/2014 09:32:15 PM · #23533

Yes, your reign as winner was so brief it was less than the time it takes for light to travel 1mm through ordinary space.

Spork wins for eternity

beatabg

Google Pixel

01/28/2014 10:59:06 PM · #23534

Eternity? Nice name :P
I win.

skewsme

Canon EOS-6D

01/28/2014 11:36:40 PM · #23535

eternity is a girly man with a steely gaze, clad in stylish underwear and some strong perfume

beatabg

Google Pixel

01/29/2014 12:50:37 AM · #23536

I wouldn't really like to meet him but I enjoyed your description. You should write a book! I kind of want to keep reading.

Canon EF-S 18-55mm f/3.5-5.6 USM

01/29/2014 01:21:00 AM · #23537

I. Am. Eternity. (but without the stylish underwear)

RayEthier

Canon EOS-5D Mark II

01/29/2014 01:52:25 AM · #23538

Originally posted by Art Roflmao:

I. Am. Eternity. (but without the stylish underwear)

Eternity should be going to bed soon or tomorrow will be today and even strong perfume won't help you. :O)

Ray

Canon EF-S 18-55mm f/3.5-5.6 USM

01/29/2014 04:07:41 AM · #23539

Take a whiff. I am in it to win it.

RayEthier

Canon EOS-5D Mark II

01/29/2014 05:14:55 AM · #23540

... and I will see your Axe and raise you a Pepe

... hehehe.

Ray

01/29/2014 07:31:27 AM · #23541

I win, that's what's up. :P

01/29/2014 08:39:42 AM · #23542

My what big ears you have...

I win

01/29/2014 08:43:05 AM · #23543

Wabbit season.

Spork wins.

01/29/2014 01:47:43 PM · #23544

waskilly wabbit

01/29/2014 03:25:30 PM · #23545

Da wabbit fwoze.

Spork wins.

01/29/2014 03:34:30 PM · #23546

bbbbbbrrrrrr It is cold down here but we missed the snow...It all went south of me

Sony DT 18-70mm f/3.5-5.6 Aspherical ED Zoom Lens for Sony Alpha

01/29/2014 04:46:23 PM · #23547

the99

Sony DSLR-A100

01/29/2014 06:59:16 PM · #23548

I dont think so ....

bvy

Sigma DP1x

01/31/2014 03:08:28 PM · #23549

Originally posted by bvy:

Originally posted by bvy:
Hi. Sorry for my absence. I've been thinking a lot about the next problem, and I finally cracked it last night during a fitful sleep. Given k >= 0, let P_k denote the family of all k-degenerate graphs, and for some graph G, let X_(P_k)(G) represent the minimum number of partitions of the vertices of V(G) necessary for each partition to induce a k-degenerate subgraph of G. A graph G is said to be l-critical with respect to X_(P_k) if X_(P_k)(G) = l but X_(P_k)(G - v) = l - 1 for every v in G. I intend to show that d(G) >= (k + 1)(l - 1).

Wow, no one caught that. The last statement is unqualified. It should read:

I intend to show that if G is l-critical with respect to X_(P_k) then d(G) >= (k + 1)(l - 1).

Perhaps there's some confusion about k-degenerate graphs and l-criticality. Consider, for example, K7, the complete graph on seven vertices. Any two partitions of the vertices of K7 will necessarily include one that contains four or more vertices. Hence the induced subgraph will necessarily contain K4 which is 3-degenerate. Therefore X_(P_2)) = 3 as shown.

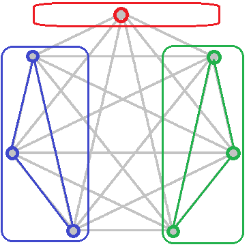
Further, K7 is 3-critical with respect to X_(P_2)); the removal of any vertex of K7, results in K6 which is 2-critical with respect to X_(P_2)) -- i.e. we could remove (without loss of generality) the single vertex partition and still need at least two, not three, partitions to induce 2-degenerate subgraphs. Observe, though, that K8 is not 3-critical with respect to X_(P_2)). Three partitions of K8 are also needed to induce 2-degenerate subgraphs, but the removal of any one vertex brings us back to the case of K7 for which X_(P_2) = 3. We can generalize that for p >= 3, that Kp (the complete graph on p vertices) is [ceil(k/3)]-critical with respect to X_(P_2)) whenever p % 3 = 1. We can further generalize that for r >= 0, Kp is [ceil(k/r)]-critical with respect to X_(P_(r - 1))) whenever p % r = 1.