| Author | Thread |
|
|
02/13/2015 09:38:45 AM · #26776 |
Originally posted by tnun:
overfull corollas do NOT hold up, not once, not again. 2nd class is 2nd class. |
If Fart Room Al were still among us, we'd have a picture to illustrate what you mean...
|
|
|
|
02/13/2015 10:29:56 AM · #26777 |
| I,ll go get them out, in wa winning way. |
|
|
|
02/13/2015 02:59:48 PM · #26778 |
I just learned that the Petersen Graph is strongly regular.
I wonder what it's trick is. Maybe it needs lots of coffee to keep straight all the edge and color requirements. |
|
|
|
02/14/2015 11:21:44 AM · #26779 |
Im makin that over-time money....I win
|
|
|
|
02/14/2015 11:49:43 AM · #26780 |
Originally posted by Jules1x:
I just learned that the Petersen Graph is strongly regular.
I wonder what it's trick is. Maybe it needs lots of coffee to keep straight all the edge and color requirements. |
Indeed it is strongly regular. A regular graph is strongly regular if every two adjacent vertices has exactly x neighbors, and every two non-adjacent vertices has exactly y neighbors, for some positive integers x and y.
I'm preparing some graphics to demonstrate my constructive proof that the Petersen graph is of class 2. |
|
|
|
02/14/2015 01:02:24 PM · #26781 |
If Petersen's a class 2,
then Thorvaald is a six;
but as for me, I graph my life
in pick-up stix...
It's been a heady journey,
and the math of it's intense;
just graph your life with a dogwood knife
like mine, and it makes sense...
I'm glad I met you, beavy,
though math guys are such nerds;
now, 'scuse me please while I try to freeze
my win with a flood of words... |
|
|
|
02/15/2015 11:40:23 AM · #26782 |
I've inspired poetry! How flattering.
Our constructive proof that the Petersen graph is class 2 will be by contradiction. Let's assume the Petersen graph is class 1 and requires a minimum of three colors to properly color its edges. (Remember the Petersen graph is 3-regular and so the maximum degree of any of its vertices is 3.)
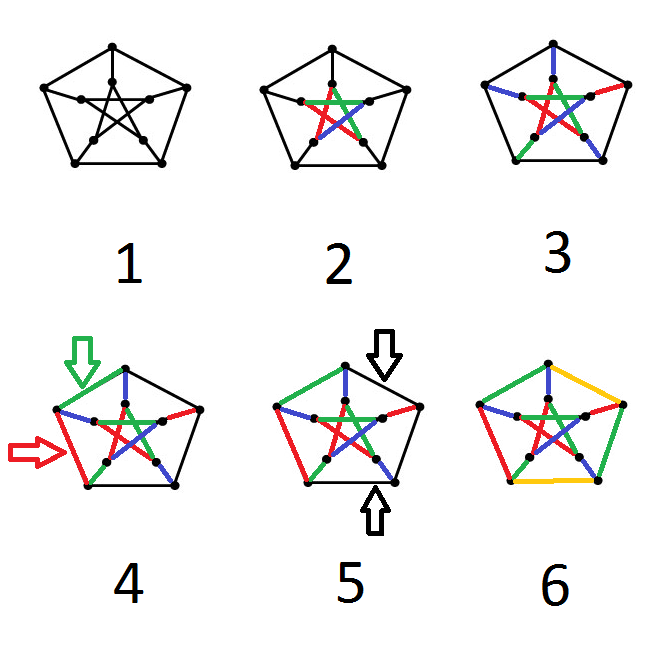
1. This is the classical representation of the Petersen graph. It can be drawn in other ways (different embeddings), but we'll stick with this most familiar one. Let's attempt to color its edges using three colors -- red, green and blue.
2. First, let's color the edges of the inner star, which is really just C5. We know that every cycle of odd degree requires three colors to properly color its edges (Ck is class 2 when k is odd because it's a regular graph of odd order.) We color its edges red-green-red-green-blue as shown.
3. Next we color the five "spokes." As no two spokes are adjacent, we simply (and necessarily) assign to each edge whatever color is not assigned to its two colored adjacent edges in the star.
4. Now we attempt to color the edges of the perimeter. Starting in the lower left and moving clockwise, we again must color the edges with whatever color is not assigned to an adjacent edge. We can do this with two edges, but then we run into a problem.
5. The two edges indicated here have adjacent edges which use each of the three colors available to us. A fourth color is required. Hence we've arrived at a contradiction, and the Petersen graph cannot be class 1.
6. Here we show the edges of the Petersen graph properly colored using the minimum of four colors.
Message edited by author 2015-02-15 12:20:21. |
|
|
|
02/15/2015 06:02:21 PM · #26783 |
| Perhaps at step 5, we could have stopped and noticed that any edge in the perimeter would have to be adjacent to a blue spoke. Therefore no edge in the perimeter could be colored blue. That leaves only two colors to color the edges of the perimeter, which is C5, and that, of course, is impossible. |
|
|
|
02/15/2015 06:24:43 PM · #26784 |
you need to be much faster:  |
|
|
|
02/15/2015 08:18:51 PM · #26785 |
Bah! Youse guys and your pretty pitchers
Spork wins |
|
|
|
02/16/2015 06:57:42 AM · #26786 |
I,m not sure if the mirror always tells the truth.
Another win all the same. |
|
|
|
02/16/2015 07:10:32 PM · #26787 |
| Next I will prove that a cubic Hamiltonian graph is of class 1. |
|
|
|
02/16/2015 07:17:32 PM · #26788 |
Originally posted by bvy:
Next I will prove that a cubic Hamiltonian graph is of class 1. |
Well, an elliptical ALEXANDRIAN is certainly of class 3... |
|
|
|
02/16/2015 10:01:47 PM · #26789 |
|
|
|
02/16/2015 11:25:35 PM · #26790 |
The Bear has silenced Beavey,
and his graphs have come to naught;
his plots have gone all weavey
and his axes are distraught!
Message edited by author 2015-02-16 23:26:11. |
|
|
|
02/17/2015 03:55:27 AM · #26791 |
| Best to draw a draught... axe the alexandrine graft. |
|
|
|
02/17/2015 06:15:25 PM · #26792 |
Ill have a yard of ale please
|
|
|
|
02/17/2015 06:19:52 PM · #26793 |
| a yard of ale to bail the bard |
|
|
|
02/18/2015 06:58:04 PM · #26794 |
|
|
|
02/18/2015 07:35:48 PM · #26795 |
| Hey we have a shenanigans here. Great bar |
|
|
|
02/18/2015 09:19:59 PM · #26796 |
|
|
|
02/21/2015 12:06:30 PM · #26797 |
In case you missed it...
It's actually quite easy to show that a cubic Hamiltonian graph is class 1 -- that is, that its edges can be properly colored using exactly as many colors as the maximum degree of G (which is 3). Let G be a cubic (i.e. 3-regular) Hamiltonian graph. Then G contains a Hamiltonian cycle H, with V(G) = V(H). Each vertex of G must then be adjacent to exactly two edges of H. If we remove the edges of G which are also in H, then the remaining vertices have degree 1. In other words, G - E(H) is a 1-regular graph -- or a disjoint set of edges. The order of G is then (necessarily) even, with each edge joining pairs of vertices of G. Hence, our Hamiltonian cycle H is Ck for some even k, and its edges in G can be alternatingly colored with two colors. The remaining disjoint edges of G - E(H) can be colored with a third color since none of these edges will be mutually adjacent. Hence G can be properly colored using three colors and is of class 1.
My plan is to present a few more results on edge coloring and then move into graph matchings, factors and decompositions. |
|
|
|
02/21/2015 12:26:23 PM · #26798 |
Coloring?
While Spork is sure that some of the people in "Last wins" have not moved beyond crayons and coloring, you really should post something with appeal beyond the kindergarten age group.
Spork wins |
|
|
|
02/21/2015 12:38:55 PM · #26799 |
True.
But.
A
Win
For
N
Me |
|
|
|
02/21/2015 01:35:13 PM · #26800 |
The hypercube graph Qn may be constructed from the family of subsets of a set with n elements, by making a vertex for each possible subset and joining two vertices by an edge whenever the corresponding subsets differ in a single element. Equivalently, it may be constructed using 2n vertices labeled with n-bit binary numbers and connecting two vertices by an edge whenever the Hamming distance of their labels is 1. These two constructions are closely related: a binary number may be interpreted as a set (the set of positions where it has a 1 digit), and two such sets differ in a single element whenever the corresponding two binary numbers have Hamming distance 1.
Alternatively, Qn+1 may be constructed from the disjoint union of two hypercubes Qn, by adding an edge from each vertex in one copy of Qn to the corresponding vertex in the other copy, as shown in the figure. The joining edges form a perfect matching.
Another definition of Qn is the Cartesian product of n two-vertex complete graphs K2. |
|
Home -
Challenges -
Community -
League -
Photos -
Cameras -
Lenses -
Learn -
Help -
Terms of Use -
Privacy -
Top ^
DPChallenge, and website content and design, Copyright © 2001-2025 Challenging Technologies, LLC.
All digital photo copyrights belong to the photographers and may not be used without permission.
Current Server Time: 12/23/2025 02:35:44 PM EST.

