| Author | Thread |
|
|
05/20/2013 01:52:07 PM · #21151 |
| Total protonic reversal. I win. |
|
|
|
05/20/2013 03:06:30 PM · #21152 |
|
|
|
05/20/2013 03:12:39 PM · #21153 |
|
|
|
05/20/2013 03:15:13 PM · #21154 |
Originally posted by Art Roflmao:
Total protonic reversal. I win. |
That caused both a time shift and a rift between two parallel universes.
Art won yesterday in that universe
And will win in approximately 350 million years here, but only for one millisecond.
At all other times, Spork wins |
|
|
|
05/20/2013 03:15:26 PM · #21155 |
|
|
|
05/20/2013 03:17:20 PM · #21156 |
| Spork is winning...only Spork. |
|
|
|
05/20/2013 03:19:09 PM · #21157 |
|
|
|
05/20/2013 03:24:33 PM · #21158 |
Originally posted by bvy:
Would a picture help? |
Pictures result in losing.
Spork wins |
|
|
|
05/20/2013 03:26:46 PM · #21159 |
you are losing...I am winning
|
|
|
|
05/20/2013 03:42:48 PM · #21160 |
| Picture this: Me, winning. |
|
|
|
05/20/2013 04:14:32 PM · #21161 |
Originally posted by Art Roflmao:
Picture this: Me, winning. |
That was easy, Spork wins |
|
|
|
05/20/2013 04:29:53 PM · #21162 |
|
|
|
05/20/2013 05:15:20 PM · #21163 |
Originally posted by bvy:
Would a picture help? |
Yup I'd love to see a picture |
|
|
|
05/20/2013 05:15:39 PM · #21164 |
quit being so easy, Art....
|
|
|
|
05/20/2013 05:16:47 PM · #21165 |
Originally posted by Art Roflmao:
 |
We went over this art wins,  Art Roflmao doesn't. Art Roflmao doesn't. |
|
|
|
05/20/2013 06:03:43 PM · #21166 |
|
|
|
05/20/2013 06:04:55 PM · #21167 |
|
|
|
05/20/2013 06:09:41 PM · #21168 |
By request...
 |
|
|
|
05/20/2013 06:31:04 PM · #21169 |
That's a dangerous game you're playing.
 |
|
|
|
05/20/2013 06:34:20 PM · #21170 |
Bring it.
 |
|
|
|
05/20/2013 06:40:04 PM · #21171 |
| I think you're both scary enough to qualify for a drone strike. |
|
|
|
05/20/2013 07:28:46 PM · #21172 |
|
|
|
05/20/2013 08:03:05 PM · #21173 |

Now it's a party. |
|
|
|
05/20/2013 09:22:38 PM · #21174 |
|
|
|
05/20/2013 09:52:51 PM · #21175 |
Originally posted by bvy:
My most recent exploration into graph theory involves vertex colorings. The problem du jour is stated as follows: Let G be a k-chromatic graph and r = D(G). (Here D(G) signifies capital delta of G, the maximum degree of any vertex of G.) Show that there exists a k-chromatic r-regular graph H, which has G as an induced subgraph.
Assuming that G itself is not a regular graph (the trivial case), there is some vertex v which has degree strictly less than D(G). To "regularize" this vertex, v must add exactly D(G) - deg(v) edges to vertices of H which are not also vertices of G. This must be done for all vertices of G having degree less than D(G).
So constructing H is a matter of adding new vertices and edges which regularize all of the "smaller" vertices of G. The two caveats to this are: one, the new vertices of H must each have degree exactly D(G), and two, we must not add edges in a way that increases the chromatic number of H beyond that of G.
Thoughts or insight? |
Thanks for your help, everyone. As promised, here's a picture. As an example, I'm using the graph G=T(4,1) since it has vertices of degree 1, 2 and 3. It has chromatic number two as shown by the red and green vertices. To construct H, I partitioned its would-be vertices by color -- necessarily, red and green. This picture is the first step, and I will complete it later.
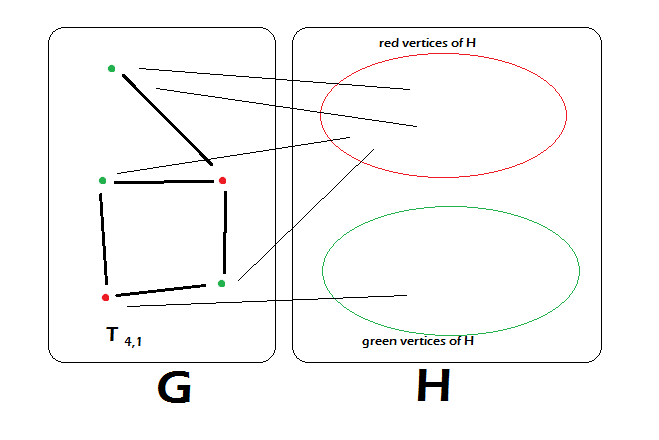
The picture shows only one edge going to a green vertex of H. So if H is to have a green vertex, and be 3-regular, it needs two more edges. Those will necessarily be adjacent to red vertices in H. Do you see where this is going? |
|
Home -
Challenges -
Community -
League -
Photos -
Cameras -
Lenses -
Learn -
Help -
Terms of Use -
Privacy -
Top ^
DPChallenge, and website content and design, Copyright © 2001-2025 Challenging Technologies, LLC.
All digital photo copyrights belong to the photographers and may not be used without permission.
Current Server Time: 11/21/2025 06:33:56 PM EST.

