| Author | Thread |
|
|
01/28/2011 04:30:50 AM · #4926 |
| Not very much... I usually sleep between 6pm and midnight your time. Any other time, I'm awake to bother you and everyone else. Muh ha ha ha |
|
|
|
01/28/2011 12:47:57 PM · #4927 |
Aaaarrrrreeeee....you are getting sleeeeeppyyyy! :P
:D |
|
|
|
01/28/2011 03:23:55 PM · #4928 |
A planar graph G is maximally connected if the addition of any edge to G will make it non-planar. Such a graph is also said to be triangulated (each region, including the outer region, is bound by exactly three edges). Given a triangulated graph G of order k, with k >= 4, we show that the minimum degree of any of its vertices is three. The proof is by induction on k.
The complete graph on four vertices, K4, is planar and obviously triangulated, and the degree of each of its vertices is three. Consider a triangulated graph G of order k, with k > 4. By our induction hypothesis, the degree of each of its vertices is at least three. We add a vertex v to G to obtain a graph of order k + 1. Any region to which v is added (including the external region) must be bound by at least (actually exactly) three vertices. So we add edges connecting v to at least three other vertices. Hence, v also has degree at least three, and our inductive step is satisfied.
We will use this result later.
|
|
|
|
01/28/2011 06:23:07 PM · #4929 |
|
|
|
01/29/2011 03:06:05 AM · #4930 |
| Sounds to me like he has issues. Starting to think he's socially inept. |
|
|
|
01/29/2011 08:50:10 AM · #4931 |
|
|
|
01/30/2011 02:48:53 AM · #4932 |
|
|
|
01/30/2011 03:29:33 AM · #4933 |
|
|
|
01/30/2011 12:26:06 PM · #4934 |
I'mmmm Uuuuup!
Morning kiddos! Can't chat...got pics to work! Laters!!!! :~D |
|
|
|
01/30/2011 09:36:28 PM · #4935 |
Originally posted by bvy:
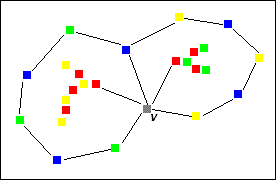
The vertices incident with v are green, red, blue, red, yellow. You can see a green-blue Kempe chain surrounding one red vertex and a yellow-blue chain surrounding the other red vertex. Kempe reasoned that since both red vertices were surrounded, that a red-yellow chain of the first red vertex, and a red-green chain of the second, can have their colors inverted allowing v to be colored red. Casually stated. Do you see the flaw in Kempe's reasoning? |
The diagram below indicates the flaw in Kempe's reasoning.
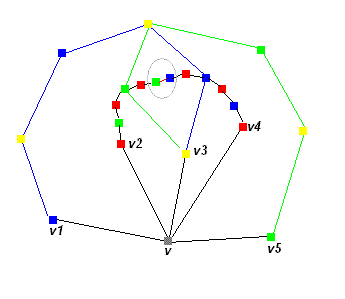
(I apologize that I changed the order of the colors assigned to the vertices incident to v from the original diagram. There should, however, be no loss of generality.)
Here you see a blue-yellow Kempe chain surrounding v2 (red) and a green-yellow chain surrounding v4 (red). However, that the two chains utilize a common color, means that they can enclose a common area as shown. That being the case, the red-green chain which originates from v2, and the red-blue chain which originates from v4, can meet up -- i.e. they cannot be completely isolated as Kempe reasoned. Inverting the colors of each of the red-green and red-blue chains in the diagram creates a contradiction at the spot circled in light gray: The two vertices joined by the red edge, both become red.
It is in exactly this situation that Kempe's reasoning falls apart. Good evening. |
|
|
|
01/30/2011 11:35:30 PM · #4936 |
| the top diagram looks like a swim suit top! |
|
|
|
01/31/2011 10:42:46 AM · #4937 |
| Morning...how is everyone...no need to answer... |
|
|
|
01/31/2011 05:10:10 PM · #4938 |
Where's Art?
Send out the search party! |
|
|
|
01/31/2011 08:54:11 PM · #4939 |
| he must be on sabbatical yet once again...he swears us off then comes crawling back....hmmm |
|
|
|
01/31/2011 09:07:22 PM · #4940 |
Originally posted by bergiekat:
the top diagram looks like a swim suit top! |
Thank you!
Later this week, I'll be demonstrating that all planar graphs of order greater than three, have at least four vertices of degree five or less. |
|
|
|
01/31/2011 09:51:03 PM · #4941 |
Originally posted by bvy:
There should, however, be no loss of generality.)
|
Ha! I lost the generality years ago.
Message edited by author 2011-01-31 21:51:28. |
|
|
|
02/01/2011 08:53:23 AM · #4942 |
| Morning...got no coffee...YET |
|
|
|
02/03/2011 01:25:57 AM · #4943 |
| Evening, kids...my feet are cold! |
|
|
|
02/03/2011 09:13:51 AM · #4944 |
| good morning all - Janine have you found that coffee yet? |
|
|
|
02/03/2011 09:53:02 AM · #4945 |
Originally posted by eva2k0:
good morning all - Janine have you found that coffee yet? |
finally...I'm back at home and found the pot and beans... :) life is good |
|
|
|
02/03/2011 03:48:20 PM · #4946 |
| I need to make some coffee! But I'd rather take a nap! |
|
|
|
02/03/2011 08:07:30 PM · #4947 |
Oh dear, oh dear.. why cant i go to sleep!!
|
|
|
|
02/03/2011 11:39:40 PM · #4948 |
|
|
|
02/04/2011 07:57:01 AM · #4949 |
| at this point...not enough...Morning |
|
|
|
02/04/2011 07:59:32 AM · #4950 |
| just enough coffee, just enough sleep, already a productive day @ work, TGIF |
|
Home -
Challenges -
Community -
League -
Photos -
Cameras -
Lenses -
Learn -
Help -
Terms of Use -
Privacy -
Top ^
DPChallenge, and website content and design, Copyright © 2001-2025 Challenging Technologies, LLC.
All digital photo copyrights belong to the photographers and may not be used without permission.
Current Server Time: 11/18/2025 08:46:16 AM EST.

